Trigonometric Identities

As math students and future teachers, we all have to memorize all the different Trigonometric Identities. With this simple diagram you are able to get 21 different Trigonometric Identities with four different tricks. If I was presented this diagram in High School (this was presented to me in my college education class), I would have been able to memorize some of the Trigonometric Identities a lot faster. Below is the Trig Identity Trick:

Now I will break down each one of the four tricks in this one diagram. The first trick is finding the Reciprocal Identities. 

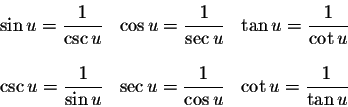
We will follow the red lines in the diagram. From the start of one identity on the line equals 1 divided by the end identity of line. 

 The second trick is finding the Pythagorean Identities. 

We will now look at the triangles. We will look at the left corner of the triangle and travel around the triangle clockwise. The point of the triangle is what the Pythagorean Identity is equal to and the top two points are added together. Remember that all the identities are squared!

The last two tricks go hand in hand. The third and fourth trick is finding the Quotient Identities and relations of the other identities.

Quotient Identities

Other Relations 

going around clockwise

going around counter clockwise

This is a great tool in which students and teachers can use all through out Trigonometry. This will relieve stress in memorizing all the trigonometric identities and focus more on applying the identity to problems. This graph is a great tool to use int he classroom because it uses only the six basic Trig Identities and creates many different formulas that they students will use multiple times through out the life time of math. Instead of the students memorizing all the different formulas they just have to remember how to construct this graph and how to use it. All of the formals are within this graph!